Régression géographiquement pondérée

Avant-propos

Les données de transcations immobilières utilisées ici (données DVF, pour Demandes de Valeurs Foncières), disponibles sous licence ouverte depuis 2019, sont réputées globalement fiables et exhaustives, mais nécessitent néanmoins des précautions d’utilisation (voir une description de leur qualité ici : https://www.groupe-dvf.fr/vademecum-fiche-n3-precautions-techniques-et-qualite-des-donnees-dvf/). La base utilisée ci-dessous a été retravaillée par etalab, un département de la direction interministérielle du numérique.

L’utilisation de ce jeu de données est ici réalisé dans un but exclusivement pédagogique, et non académique. Par conséquent, la qualité de la donnée n’a pas été re-vérifiée de façon approfondie, et il convient de rester prudent quant aux inférences issues de ces analyses.

1 Objectif de ce support

L’objectif est de mettre en pratique, dans R, certains des concepts et méthodes fréquemment employés en analyse spatiale, avec un focus ici sur l’hétérogénéité spatiale et la régression géographiquement pondérée (GWR). Ce support avait été présenté à l’école d’été SIGR en juillet 2021 (organisée par l’UMS RIATE) et est également disponible en tant que fiche Rzine ici : https://sigr2021.github.io/gwr/

L’hétérogénéité spatiale fait partie de deux principaux concepts de l’analyse spatiale (aux côtés de la dépendance spatiale). Cette hétérogénéité est ubiquiste et systématique, et a pour conséquence qu’aucun lieu sur terre ne saurait être représentatif de tous les autres. Elle a un rôle fondamental dans les analyses géographiques, en particulier quantitatives (elle est indissociable des problèmes de représentativité spatiale, de résolution et d’échelle d’analyse).

D’un point de vue statistique, la traduction de l’hétérogénéité spatiale est la non-stationnarité spatiale. Celle-ci désigne l’instabilité, dans l’espace, des moyennes, des variances et des covariances. La non-stationnarité spatiale des covariances fait référence à l’hétérogénéité spatiale des relations statistiques. C’est cet élément qui fait l’objet de la démonstration ci-dessous.

L’hétérogénéité spatiale des relations statistiques est très fréquente, dans de nombreux domaines (écologie, santé, économie, etc.), et son ignorance peut induire des erreurs d’interprétation importantes et des conséquences économiques et sanitaires (par exemple) non négligeables.

Dans le domaine des marchés immobiliers, cette hétérogénéité spatiale des relations est habituelle. Par exemple, on sait que l’effet marginal d’1 m\(^2\) supplémentaire sur le prix de vente est variable selon la localisation (typiquement plus élevé en zone dense, dans les centres-villes). Cela a des conséquences sur l’estimation des marchés, mais aussi en modélisation hédonique, sur l’estimation de la valeur de différentes caractéristiques sur la base de ces relations.

Cela a poussé des auteurs à segmenter les marchés immobiliers en sous-marchés homogènes, au sein desquels les déterminants du prix seraient stationnaires (voir par exemple Goodman et Thibodeau (1998) ou Helbich et al. (2013)). La question est de savoir comment délimiter ces sous-marchés de façon pertinente.

La méthode proposée dans le cadre de ce cours, la GWR, est une méthode de régression locale qui permet précisément d’explorer la non-stationarité spatiale à travers des cartes de relations (Fotheringham et al., 2003), et de servir alors de base pour une régionalisation. Nous allons préciser la façon dont ce type de modèle est calibré, estimé et interprété.

2 Import et préparation de la base

# Chargement des librairies
library(tidyverse)
library(sf)
library(tmap)
library(plotly)
library(gtsummary)
library(GGally)
library(GWmodel)
library(spdep)

La base est disponible et décrite ici : https://www.data.gouv.fr/fr/datasets/demandes-de-valeurs-foncieres-geolocalisees/

On importe directement le csv dans R (pour le département 17) :

# Import de la base brute
data <- read_csv("https://files.data.gouv.fr/geo-dvf/latest/csv/2020/departements/17.csv.gz")

# Vérifier que l'import est correct
head(data)
# A tibble: 6 × 40
  id_mutation date_mutation numero_disposition nature_mutation valeur_fonciere
  <chr>       <date>        <chr>              <chr>                     <dbl>
1 2020-114158 2020-07-01    000001             Vente                    576000
2 2020-114159 2020-07-01    000002             Vente                    200000
3 2020-114160 2020-07-01    000001             Vente                    540800
4 2020-114160 2020-07-01    000001             Vente                    540800
5 2020-114161 2020-07-01    000001             Vente                    162000
6 2020-114162 2020-07-02    000001             Vente                     43000
# ℹ 35 more variables: adresse_numero <dbl>, adresse_suffixe <chr>,
#   adresse_nom_voie <chr>, adresse_code_voie <chr>, code_postal <dbl>,
#   code_commune <dbl>, nom_commune <chr>, code_departement <dbl>,
#   ancien_code_commune <lgl>, ancien_nom_commune <lgl>, id_parcelle <chr>,
#   ancien_id_parcelle <lgl>, numero_volume <dbl>, lot1_numero <dbl>,
#   lot1_surface_carrez <dbl>, lot2_numero <dbl>, lot2_surface_carrez <dbl>,
#   lot3_numero <dbl>, lot3_surface_carrez <lgl>, lot4_numero <lgl>, …
# Filtre sur les ventes de maisons à Oléron avec coordonnées géographiques
dataOleron <- data %>% 
  filter(nom_commune %in% c("Dolus-d'Oléron",
                            "La Brée-les-Bains",
                            "Le Château-d'Oléron",
                            "Le Grand-Village-Plage",
                            "Saint-Denis-d'Oléron",
                            "Saint-Georges-d'Oléron",
                            "Saint-Pierre-d'Oléron",
                            "Saint-Trojan-les-Bains") & 
           nature_mutation == "Vente" & 
           type_local == "Maison" &
           !is.na(longitude) & 
           !is.na(surface_terrain) &
           !is.na(valeur_fonciere))
# Conversion en *sf*
dataSf <- dataOleron %>% 
  st_as_sf(coords = c("longitude","latitude"), 
           crs = 4326) # WGS84

plot(st_geometry(dataSf))

# Import du fond de carte en shapefile
oleron <- st_read("data/oleron.shp")
Reading layer `oleron' from data source 
  `/data/user/f/tfeuillet/coursQmd/data/oleron.shp' using driver `ESRI Shapefile'
Simple feature collection with 1 feature and 1 field
Geometry type: LINESTRING
Dimension:     XY
Bounding box:  xmin: -1.413073 ymin: 45.79904 xmax: -1.187825 ymax: 46.04829
Geodetic CRS:  WGS 84
# Cartographie
tmap_mode("view")
ℹ tmap modes "plot" - "view"
ℹ toggle with `tmap::ttm()`
tm_shape(oleron) + 
  tm_lines(col = "black") + 
  tm_shape(dataSf) + 
  tm_dots(fill = "red")
# Ajout d'une variable contextuelle : distance au littoral
dataSf$dist_litt <- st_distance(dataSf, oleron) %>% 
  as.numeric()

3 Exploration des variables

3.1 Distribution de la variable dépendante (prix de vente)

plot_ly(dataSf, x = ~valeur_fonciere) %>% add_histogram()
# Suppression d'une valeur aberrante
dataSf <- dataSf %>% filter(valeur_fonciere > 1000)
# Distribution très dissymétrique
plot_ly(dataSf, x = ~log(valeur_fonciere)) %>% add_histogram()

C’est mieux !

3.2 Distribution des variables indépendantes

a <- plot_ly(dataSf, x = ~log(dist_litt)) %>% add_histogram()
b <- plot_ly(dataSf, x = ~log(surface_reelle_bati)) %>% add_histogram()
c <- plot_ly(dataSf, x = ~log(surface_terrain)) %>% add_histogram()
subplot(a,b,c)
# Suppression des maisons vraisemblablement trop petites
dataSf <- dataSf %>% filter(surface_reelle_bati > 10)

# Création des variables log (pour faciliter la carto par la suite)
dataSf$log_valeur_fonciere <- log(dataSf$valeur_fonciere)
dataSf$log_dist_litt <- log(dataSf$dist_litt)
dataSf$log_surface_reelle_bati <- log(dataSf$surface_reelle_bati)
dataSf$log_surface_terrain <- log(dataSf$surface_terrain)

4 Relations bivariées - formes fonctionelles

ggplot(dataSf, aes(x=log(dist_litt), y=log(valeur_fonciere))) + 
  geom_point() + geom_smooth()

ggplot(dataSf, aes(x=log(surface_reelle_bati), y=log(valeur_fonciere))) + 
  geom_point() + geom_smooth()

ggplot(dataSf, aes(x=log(surface_terrain), y=log(valeur_fonciere))) + 
  geom_point() + geom_smooth()

5 Modèle log-log global (MCO)

mco <- lm(log_valeur_fonciere ~ log_dist_litt + log_surface_reelle_bati + log_surface_terrain, data = dataSf)
mco %>%
  gtsummary::tbl_regression(intercept = TRUE) %>% 
  add_vif()
Characteristic Beta 95% CI p-value VIF
(Intercept) 10 9.5, 10 <0.001
log_dist_litt -0.08 -0.12, -0.05 <0.001 1.0
log_surface_reelle_bati 0.35 0.26, 0.43 <0.001 1.2
log_surface_terrain 0.25 0.22, 0.29 <0.001 1.2
Abbreviations: CI = Confidence Interval, VIF = Variance Inflation Factor 
ggcoef_model(mco)

  • Cartographie des résidus
dataSf$resMco <- mco$residuals

tm_shape(dataSf) + 
  tm_dots(col = "resMco", 
          style = "quantile",
          palette = "-RdYlBu")

6 Modèle GWR

6.1 Principes généraux

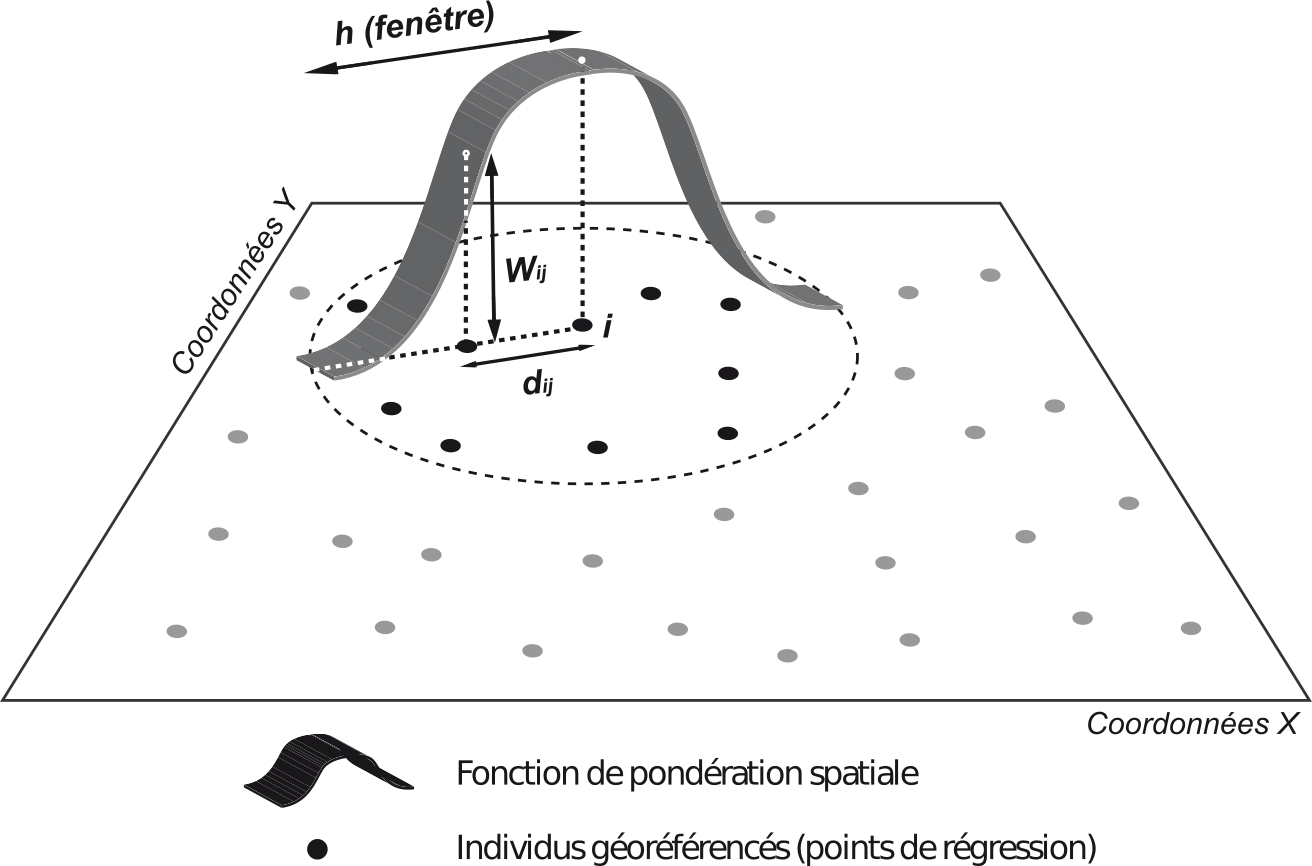
Source : Feuillet et al. (2019)

6.2 Calibration du modèle : définition et pondération du voisinage

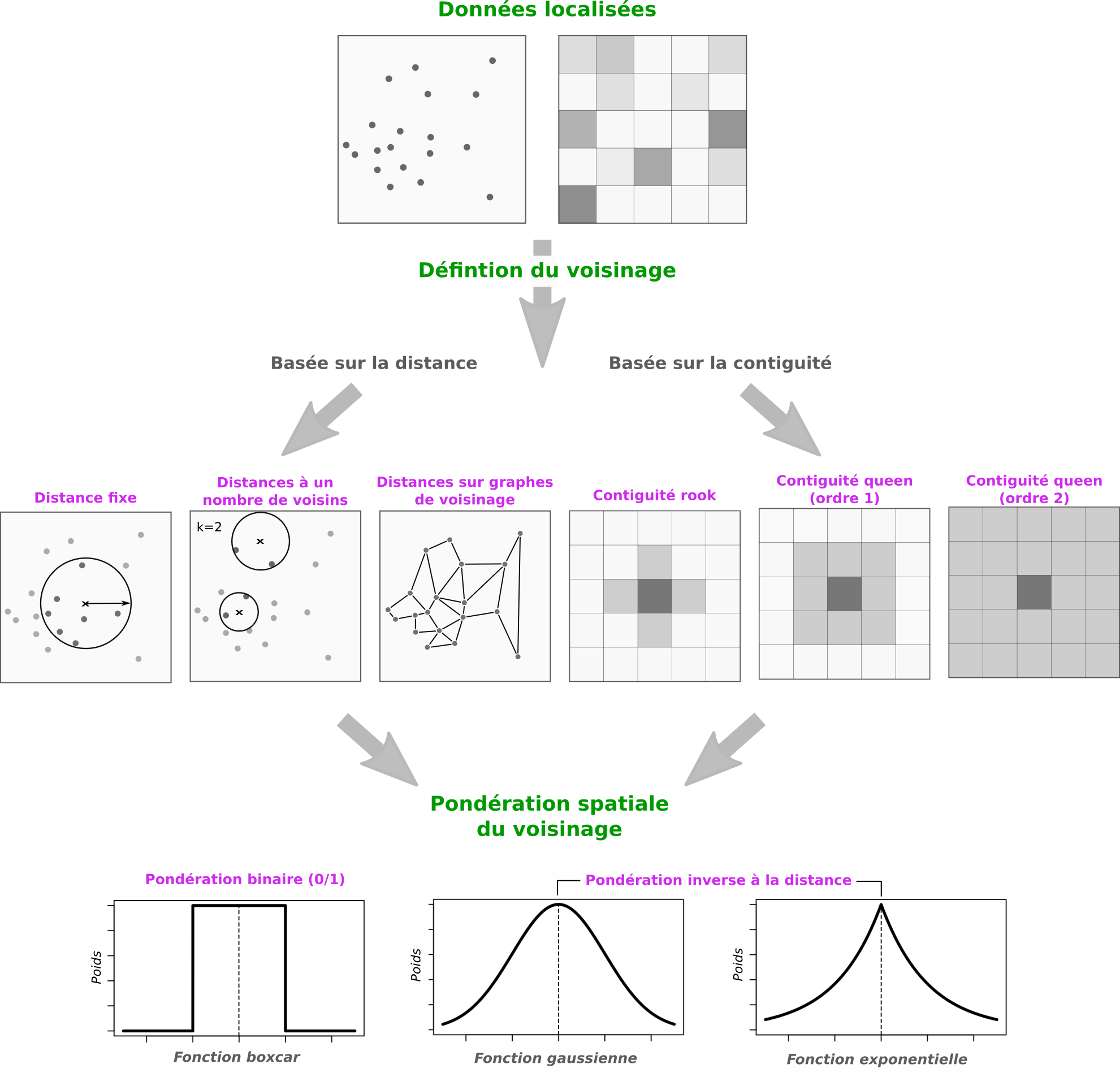
Source : Feuillet et al. (2019)

  • Première chose à faire : convertir l’objet sf en objet sp
dataSp <- as_Spatial(dataSf) # le package GWmodel n'est pas compatible avec 'sf'

6.2.1 Construction de la matrice de distances

matDist <- gw.dist(dp.locat = coordinates(dataSp))

6.2.2 Optimisation du voisinage (h)

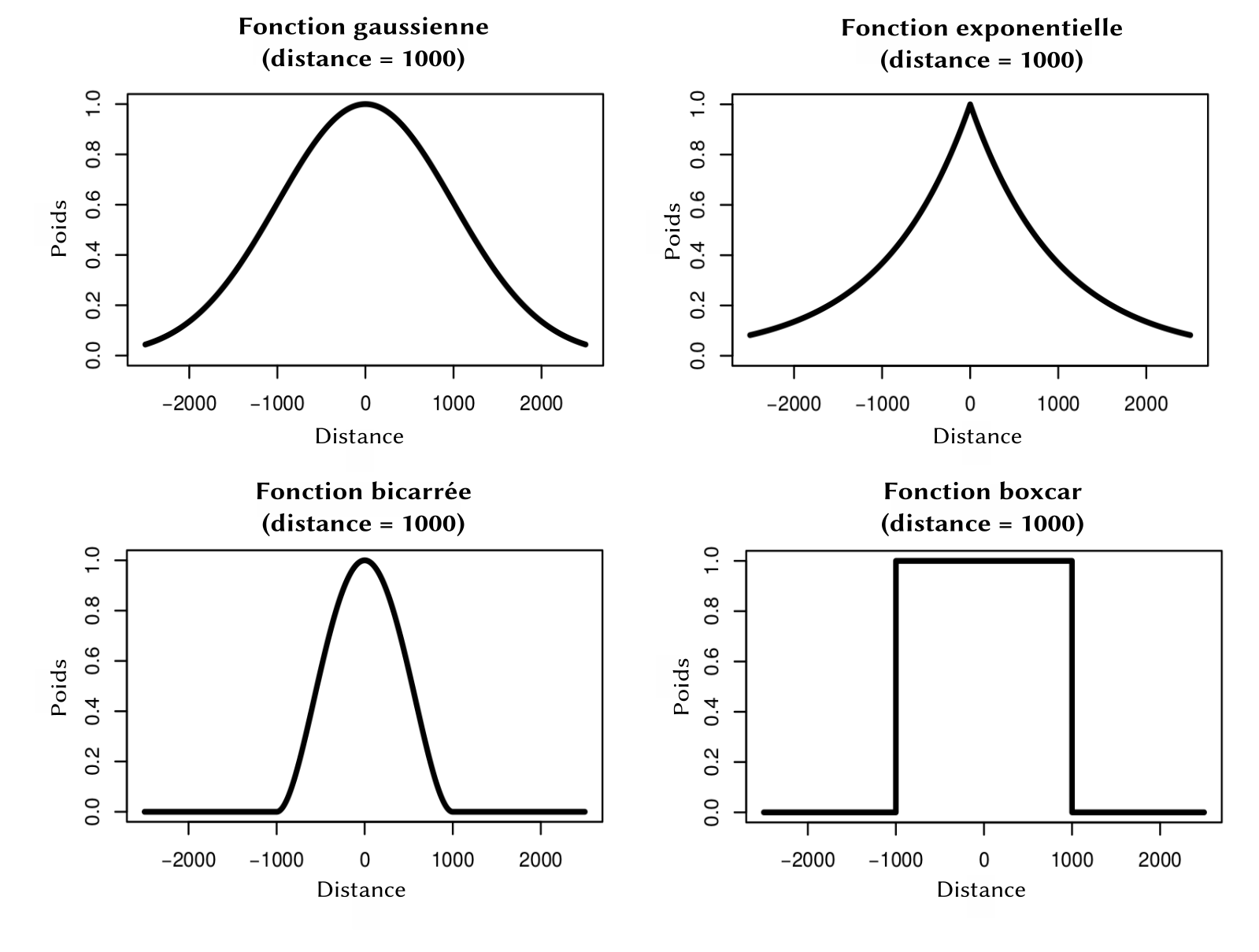
Source : Feuillet et al. (2019)

  • Comparaison de deux pondérations spatiales : exponentielle et bicarrée :
# Exponential
nNeigh.exp <- bw.gwr(data = dataSp, approach = "AICc",
                     kernel = "exponential",
                     adaptive = TRUE,
                     dMat = matDist,
                     formula = log_valeur_fonciere ~ log_dist_litt + log_surface_reelle_bati + log_surface_terrain)
Adaptive bandwidth (number of nearest neighbours): 280 AICc value: 413.5651 
Adaptive bandwidth (number of nearest neighbours): 181 AICc value: 411.2085 
Adaptive bandwidth (number of nearest neighbours): 118 AICc value: 409.2994 
Adaptive bandwidth (number of nearest neighbours): 81 AICc value: 406.3428 
Adaptive bandwidth (number of nearest neighbours): 56 AICc value: 404.8269 
Adaptive bandwidth (number of nearest neighbours): 42 AICc value: 401.8334 
Adaptive bandwidth (number of nearest neighbours): 32 AICc value: 398.9798 
Adaptive bandwidth (number of nearest neighbours): 27 AICc value: 393.9232 
Adaptive bandwidth (number of nearest neighbours): 23 AICc value: 394.5678 
Adaptive bandwidth (number of nearest neighbours): 29 AICc value: 394.7075 
Adaptive bandwidth (number of nearest neighbours): 25 AICc value: 394.9863 
Adaptive bandwidth (number of nearest neighbours): 27 AICc value: 393.9232 
# Bisquare
nNeigh.bisq <- bw.gwr(data = dataSp, approach = "AICc", 
                 kernel = "bisquare", 
                 adaptive = TRUE, 
                 dMat = matDist, 
                 formula = log_valeur_fonciere ~ log_dist_litt + log_surface_reelle_bati + log_surface_terrain)
Adaptive bandwidth (number of nearest neighbours): 280 AICc value: 415.1779 
Adaptive bandwidth (number of nearest neighbours): 181 AICc value: 414.4262 
Adaptive bandwidth (number of nearest neighbours): 118 AICc value: 411.7238 
Adaptive bandwidth (number of nearest neighbours): 81 AICc value: 417.0812 
Adaptive bandwidth (number of nearest neighbours): 143 AICc value: 410.992 
Adaptive bandwidth (number of nearest neighbours): 156 AICc value: 412.5089 
Adaptive bandwidth (number of nearest neighbours): 132 AICc value: 410.2652 
Adaptive bandwidth (number of nearest neighbours): 128 AICc value: 410.4043 
Adaptive bandwidth (number of nearest neighbours): 137 AICc value: 410.9585 
Adaptive bandwidth (number of nearest neighbours): 131 AICc value: 410.2002 
Adaptive bandwidth (number of nearest neighbours): 128 AICc value: 410.4043 
Adaptive bandwidth (number of nearest neighbours): 130 AICc value: 410.2136 
Adaptive bandwidth (number of nearest neighbours): 128 AICc value: 410.4043 
Adaptive bandwidth (number of nearest neighbours): 129 AICc value: 410.1641 
Adaptive bandwidth (number of nearest neighbours): 132 AICc value: 410.2652 
Adaptive bandwidth (number of nearest neighbours): 131 AICc value: 410.2002 
Adaptive bandwidth (number of nearest neighbours): 131 AICc value: 410.2002 
Adaptive bandwidth (number of nearest neighbours): 130 AICc value: 410.2136 
Adaptive bandwidth (number of nearest neighbours): 130 AICc value: 410.2136 
Adaptive bandwidth (number of nearest neighbours): 129 AICc value: 410.1641

6.3 Estimation de la GWR

# Avec pondération exponential
GWR.exp <- gwr.basic(data = dataSp, bw = nNeigh.exp, kernel = "exponential", adaptive = TRUE,  dMat = matDist, formula = log_valeur_fonciere ~ log_dist_litt + log_surface_reelle_bati + log_surface_terrain)

# Avec pondération bisquare
GWR.bisq <- gwr.basic(data = dataSp, bw = nNeigh.bisq, kernel = "bisquare", 
                 adaptive = TRUE,  dMat = matDist, 
                 formula = log_valeur_fonciere ~ log_dist_litt + log_surface_reelle_bati + log_surface_terrain)
  • Comparaison des deux calibrations :
diagGwr <- cbind(
  rbind(nNeigh.exp,nNeigh.bisq),
  rbind(GWR.exp$GW.diagnostic$gw.R2,GWR.bisq$GW.diagnostic$gw.R2),
  rbind(GWR.exp$GW.diagnostic$AIC,GWR.bisq$GW.diagnostic$AIC)) %>% 
  `colnames<-`(c("Nb Voisins","R2","AIC")) %>% 
  `rownames<-`(c("EXPONENTIAL","BISQUARE"))
diagGwr
            Nb Voisins        R2      AIC
EXPONENTIAL         27 0.6082865 340.0876
BISQUARE           129 0.5678470 372.1653
  • La GWR avec pondération exponentielle est la plus performante
  • Interprétation des résultats bruts de la GWR :
GWR.exp
   ***********************************************************************
   *                       Package   GWmodel                             *
   ***********************************************************************
   Program starts at: 2025-12-12 11:43:43.790761 
   Call:
   gwr.basic(formula = log_valeur_fonciere ~ log_dist_litt + log_surface_reelle_bati + 
    log_surface_terrain, data = dataSp, bw = nNeigh.exp, kernel = "exponential", 
    adaptive = TRUE, dMat = matDist)

   Dependent (y) variable:  log_valeur_fonciere
   Independent variables:  log_dist_litt log_surface_reelle_bati log_surface_terrain
   Number of data points: 442
   ***********************************************************************
   *                    Results of Global Regression                     *
   ***********************************************************************

   Call:
    lm(formula = formula, data = data)

   Residuals:
     Min       1Q   Median       3Q      Max 
-1.91270 -0.20171  0.02402  0.21625  1.33972 

   Coefficients:
                           Estimate Std. Error t value Pr(>|t|)    
   (Intercept)              9.97624    0.21722  45.927  < 2e-16 ***
   log_dist_litt           -0.08360    0.01926  -4.340 1.77e-05 ***
   log_surface_reelle_bati  0.34515    0.04169   8.279 1.51e-15 ***
   log_surface_terrain      0.25422    0.01823  13.942  < 2e-16 ***

   ---Significance stars
   Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1 
   Residual standard error: 0.3872 on 438 degrees of freedom
   Multiple R-squared: 0.4934
   Adjusted R-squared: 0.4899 
   F-statistic: 142.2 on 3 and 438 DF,  p-value: < 2.2e-16 
   ***Extra Diagnostic information
   Residual sum of squares: 65.66596
   Sigma(hat): 0.386317
   AIC:  421.5673
   AICc:  421.7049
   BIC:  30.48042
   ***********************************************************************
   *          Results of Geographically Weighted Regression              *
   ***********************************************************************

   *********************Model calibration information*********************
   Kernel function: exponential 
   Adaptive bandwidth: 27 (number of nearest neighbours)
   Regression points: the same locations as observations are used.
   Distance metric: A distance matrix is specified for this model calibration.

   ****************Summary of GWR coefficient estimates:******************
                                Min.   1st Qu.    Median   3rd Qu.    Max.
   Intercept                7.875622  9.663876 10.063743 10.220684 10.8297
   log_dist_litt           -0.209386 -0.143417 -0.065722 -0.036018  0.2240
   log_surface_reelle_bati -0.078886  0.255357  0.349362  0.413194  0.6410
   log_surface_terrain      0.162807  0.227515  0.251227  0.269914  0.3646
   ************************Diagnostic information*************************
   Number of data points: 442 
   Effective number of parameters (2trace(S) - trace(S'S)): 63.24453 
   Effective degrees of freedom (n-2trace(S) + trace(S'S)): 378.7555 
   AICc (GWR book, Fotheringham, et al. 2002, p. 61, eq 2.33): 393.9232 
   AIC (GWR book, Fotheringham, et al. 2002,GWR p. 96, eq. 4.22): 340.0876 
   BIC (GWR book, Fotheringham, et al. 2002,GWR p. 61, eq. 2.34): 113.0645 
   Residual sum of squares: 50.77133 
   R-square value:  0.6082865 
   Adjusted R-square value:  0.5427051 

   ***********************************************************************
   Program stops at: 2025-12-12 11:43:43.848609
  • Première information : le R2 du modèle GWR est > au R2 du modèle MCO (plus grande capacité à expliquer la variance de Y).
  • Seconde information : il semble exister une non-stationnarité spatiale, et même des inversions de signes pour la variable distance au littoral

Il faut maintenant cartographier les betas de chaque variable pour décrire cette non-stationnarité spatiale.

# Fonction de cartographie automatique des coefficients GWR
mapGWR <- function(spdf, var, var_TV, legend.title = "betas GWR", main.title) {
  
  if (!inherits(spdf, "sf")) {
    spdf <- st_as_sf(spdf)
  }
  
  tv <- spdf[abs(var_TV) > 1.96, ]
  
  tm_shape(spdf) +
    tm_dots(fill = var, 
            size = 0.5,
            fill.legend = tm_legend(title = legend.title),
            fill.scale = tm_scale_intervals(
              style = "quantile",
              n = 6,
              values = "-RdYlBu",  
              midpoint = 0)) +
    tm_shape(oleron) + 
    tm_lines(col = "black") +
    tm_shape(tv) + 
    tm_dots(fill = "grey40", size = 0.1) +
    tm_layout(title = main.title, 
              legend.title.size = 0.9, 
              inner.margins = 0.15) 
}
# Planche cartographique des 3 variables
a <- mapGWR(GWR.exp$SDF, 
            var = "log_dist_litt",
            var_TV = GWR.exp$SDF$log_dist_litt_TV,
            main.title = "Distance au littoral")

b <- mapGWR(GWR.exp$SDF, 
            var = "log_surface_reelle_bati",
            var_TV = GWR.exp$SDF$log_surface_reelle_bati_TV,
            main.title = "Surface bâtie")

c <- mapGWR(GWR.exp$SDF, 
            var = "log_surface_terrain",
            var_TV = GWR.exp$SDF$log_surface_terrain_TV,
            main.title = "Surface terrain")

tmap_arrange(a, b, c, ncol = 2)

Bibliographie